[ZJOI2008]骑士 （树形dp+基环树）

题目

链接：https://www.luogu.com.cn/problem/P2607

Idea

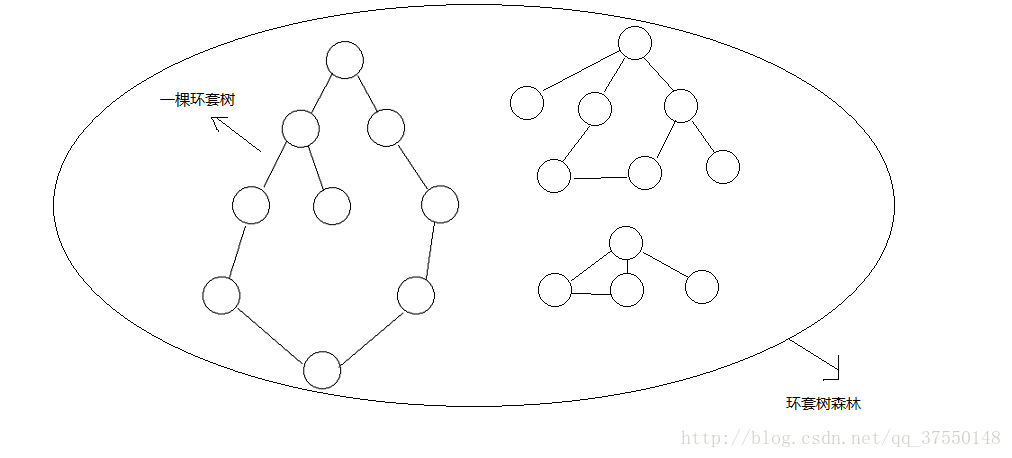
题意很清晰，没有什么恶心的地方。初看这道题，一看喜欢和不喜欢两种关系，很容易往并查集那里去想，但实际上并没有那么麻烦（当然并查集可以用），我们读完题，发现每个人都有自己的一个对头，n个人就有n种关系，我们如果把这个抽象出一幅图来，就相当于一张n个节点n条边的图（边当然是双向的），就是联通环（可能不止一个联通环）。

我们如果去掉环中的一条边，那么显然这个环就成了一棵树，这就是所谓的环套树（或者说基环树？）。

所以我们的思路是先判环，删去一条边，再从这条边的两端节点分别做树形dp，模型和没有上司的舞会基本一样。

• 判断不走断开的边时必须用边来判断，不能用点，因为两个骑士可能相互憎恨，形成重边，这时如果判断点，会造成树不联通。
• 要开long long,不然会炸。

代码细节有点问题...稍后给出...

#include <cstdio>
#include <iostream>
#include <cstring>
#define N 1000010
using namespace std;
int fun[N],a,b;
long long f[N][2];
struct node
{
    int next,to,v;
}e[2000010];
int st[1000010],vis[N],n,s,tot,x1,x2,E;
void add(int x,int y)
{
    e[tot].to=y,e[tot].next=st[x],st[x]=tot++;
    //e[++tot].to=x,e[tot].v=z,e[tot].next=st[y],st[y]=tot;
}
void find_circle(int x,int pre)
{
    vis[x]=1;
    for (int i=st[x];~i;i=e[i].next)
    {
        if ((i^1)==pre) continue;
        if (vis[e[i].to])
        {
            x1=x,x2=e[i].to;
            E=i;
            continue;
        }
        find_circle(e[i].to,i);
    }
}
void dfs(int x,int pre)
{
    f[x][0]=0;
    f[x][1]=fun[x];
    for (int i=st[x];~i;i=e[i].next)
    {
        if ((i^1)==pre) continue;
        if (i==E || (i^1)==E)
            continue;
        dfs(e[i].to,i);
        f[x][1]+=f[e[i].to][0];
        f[x][0]+=max(f[e[i].to][1],f[e[i].to][0]);
    }
}
main()
{
    memset(st,-1,sizeof st);
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
        scanf("%d%d",&a,&b),add(i,b),add(b,i),fun[i]=a;
    long long ans=0;
    for (int i=1;i<=n;i++)
    {
        if (vis[i]) continue;
        find_circle(i,-2);
        dfs(x1,-1);
        long long temp=f[x1][0];
        dfs(x2,-1);
        temp=max(temp,f[x2][0]);
        ans+=temp; 
    }
    printf("%lld",ans);
}